nextnano3 - Tutorial
next generation 3D nano device simulator
1D Tutorial
Extended Poisson-Boltzmann equation using potentials of mean force (PMF)
Author:
Stefan Birner
If you want to obtain the input file that is used within this tutorial, please
submit a support ticket.
-> 1DNaI_PMF.in
Extended Poisson-Boltzmann equation using potentials of mean force (PMF)
This tutorial uses a local dielectric constant for the electrolyte based on
the water density.
In addition, potentials of mean force (PMF) for each ion species are
taken into account to describe hydrophobic / hydrophilic interfaces.
The local dielectric constant enters the Poisson-Boltzmann equation.
Instead of assuming a constant value of eps = 78 for the
dielectric constant of water, we assume a local dielectric constant eps(z)
of water based on eq. (2) of the following paper:
[Schwierz]
Reversed Anionic Hofmeister Series: The Interplay of Surface Charge and
Surface Polarity
N. Schwierz, D. Horinek, R. R. Netz
Langmuir
26, 7370 (2010)
Here, the dielectric constant is assumed to be proportional to the water
density rho(z). This density profile has been obtained by
molecular dynamics simulations approximated by a fit function, see
[Schwierz].
The dielectric constant eps of water varies as a function of distance
z from the solid/liquid interface at z = 0 nm as
follows:
eps(z) = epsSAM + [ epsH2O
- epsSAM ] rho(z) / rho0
epsSAM = 4
(Here, we assume a self-assembled monolayer (SAM) and thus assume
a relative dielectric constant of eps = 4.)
epsH2O = 78
(dielectric constant of water)
rho0 =
(bulk density of water)
More details on the water density can be found here:
$electrolyte
==> Hydrophobic/hydrophilic (i.e. nonpolar/polar) solid/liquid interfaces.
The structure consists of 50 nm electrolyte solution containing 1 M or 10 mM
of NaI and two solid interfaces at 0 nm and 50 nm.
We use an extended Poisson-Boltzmann equation that takes into account
potentials of mean force (PMF) for each ion depending on a hydrophobic
(nonpolar) or hydrophilic (polar) solid/electrolyte interface, see eq. (1) of
[Schwierz].
$electrolyte
...
electrolyte-equation
= Poisson-Boltzmann !
!extended-Poisson-Boltzmann =
no
! (default)
extended-Poisson-Boltzmann =
PMF
!
!local-dielectric-constant
= constant-water-density !
!local-dielectric-constant
= hydrophobic
!
local-dielectric-constant
= hydrophilic
!
local-dielectric-constant-min-max = 4d0 78d0
!
The following figures show the Na+ and I-
ion concentrations contained in the file
densities/density1Dion001_ion006_M.dat (Here, 'M'
indicates that the ion density is in units of [M].)
for the following situations:
- 10 mM NaI or 1 M NaI at hydrophobic surface
- 10 mM NaI or 1 M NaI at hydrophilic surface
!local-dielectric-constant
= hydrophobic
! nonpolar interface (i.e. repelling water)
local-dielectric-constant
= hydrophilic
!
ion-name =
Na+ ! NaI
ion-name =
I- ! NaI
!ion-concentration = 10d-3 ! 10 mM
! Input: [M] = [mol/l] = 1d-3 [mol/cm^3]
ion-concentration = 1d0 ! 1 M
! Input: [M] = [mol/l] = 1d-3 [mol/cm^3]
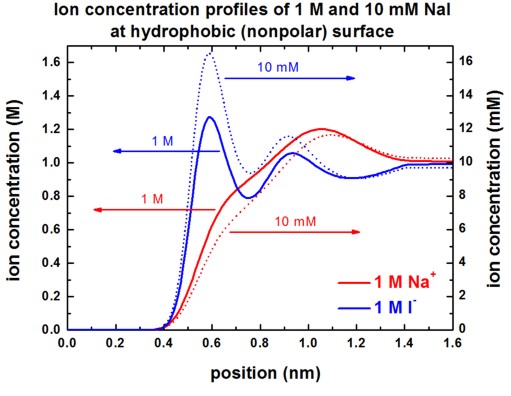
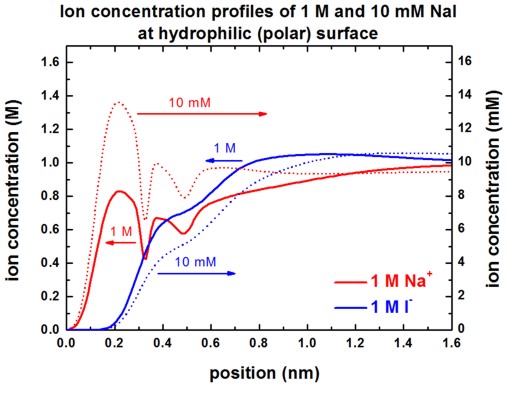
Our results are in perfect agreement with Fig. 3 (A) and Fig. 3 (C) of
[Schwierz].
The following figure shows the electrostatic potential for the hydrophobic
surface for 1 M and 10 mM NaI solutions.
band_structure/potential1D.dat
The left figure shows the potential V(z) on a linear scale, the right
figure uses a logarithmic scale and shows -V(z).
The boundary conditions for the Poisson equation were Neumann, d phi / d
z = 0, i.e. vanishing electric field.
Again, the results are in perfect agreement with Fig. 4 (A) of [Schwierz].


Potentials of mean force (PMF) for Na+ and I-
ions at hydrophobic and hydrophilic surfaces
The following figures show the PMF of Na+ and I-
ions at hydrophobic and hydrophilic surfaces in meV and kBT units.
See supplementary of [Schwierz] for more information.

|