— DEV — Interband cascade laser: gain enhancement by carrier-rebalancing¶
Header¶
- Files for the tutorial located in nextnano.NEGF\examples\quasi_equilibrium_ICLs:
ICL_zb_InAs-GaInSb_Vurgaftman_NatureComm_2011_quasi-equilibrium_moderateDoping_negf.negf
ICL_zb_InAs-GaInSb_Vurgaftman_NatureComm_2011_quasi-equilibrium_heavyDoping_negf.negf
plot_gain_*.plt
- Scope of the tutorial:
active region of ICL
optical gain
local density of states
- Relevant output files:
Init\EnergyEigenstatesFull0V\EigenStates.dat Probability distribution of eigenstates of full Hamiltonian
(Bias)mV\EnergyEigenstates\EigenStates.dat Probability distribution of eigenstates recovered from the reduced real space basis, including bias and electrostatic potential
(Bias)mV\Gain\Semiclassical_vs_Energy_(light polarization).dat Gain spectrum for each light polarization
(Bias)mV\Gain\SemiclassicalDecomposed_vs_Energy_(light polarization).dat Gain spectrum for each transition and light polarization
(Bias)mV\Gain\Semiclassical_vs_Wavelength_(light polarization).dat Gain spectrum for each light polarization
(Bias)mV\2D_plots\DensityOfStates_ZoneCenter.vtr Local density of states at the smallest in-plane momentum
(Bias)mV\2D_plots\DensityOfStates_WithDispersion.vtr Local density of states summed over in-plane momentum
(Bias)mV\2D_plots\ElectronHoleDensity_ZoneCenter.vtr Energy-resolved carrier densities at the smallest in-plane momentum
(Bias)mV\2D_plots\ElectronHoleDensity_WithDispersion.vtr Energy-resolved carrier densities summed over in-plane momentum
(Bias)mV\FermiLevels.dat Quasi-Fermi levels and the energy border for distinguishing electrons and holes
Introduction¶
This tutorial presents simulation of an active region of an interband cascade laser (ICL) following a design of [VurgaftmanNatComm2011] under quasi-equilibrium assumption, i.e., assuming that the interband transition is much slower than the intraband counterpart. The calculation includes the band bending due to carrier concentration and reproduces the carrier rebalancing by heavily doping the electron injector region, which was experimentally demonstrated in the paper. Our gain calculation based on Fermi’s golden rule confirms the resulting gain enhancement.
To produce the 1D plots (Figure 4.4.14, Figure 4.4.15, Figure 4.4.16, Figure 4.4.17), please place the corresponding plt (Gnuplot) file to the root of your output directory and run it.
Models¶
8-band \(\mathbf{k} \cdot \mathbf{p}\) model¶
An 8-band \(\mathbf{k} \cdot \mathbf{p}\) model is used to find energy eigenstates in the heterostructure grown along the simulation \(z\) axis. The non-equilibrium Green’s function (NEGF) basis is constructed from them (see SimulationParameter{ } for details).
Quasi-equilibrium assumption¶
In the mode space obtained above, nextnano.NEGF solves the NEGF equations and Poisson equation self-consistently. In this tutorial, Equilibrium{SplitFermi = yes} is used in the input file (see Input file settings) to activate the assumption that the interband transition in the recombination region (W-shaped quantum well) is much slower than the intraband process. This allows us to define constant quasi-Fermi levels for electrons and holes (Figure 4.4.11). They are split by the potential drop per period, which corresponds to device operation at 100% voltage efficiency.
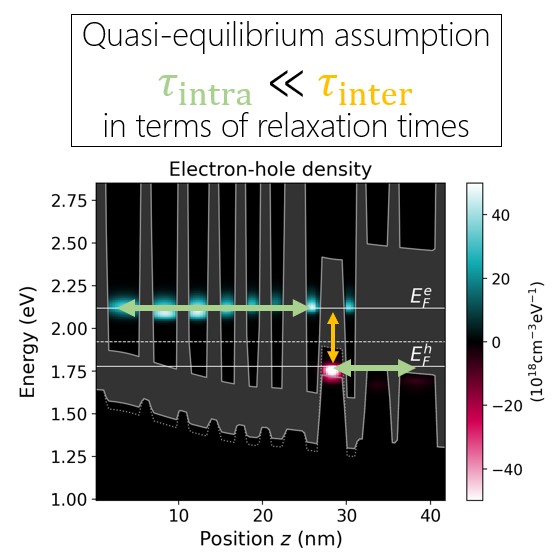
Figure 4.4.11 Quasi-equilibrium assumption is the approximation that the electrons and holes thermalize separately in the electron and hole injectors, respectively, due to interband processes being much slower than the intraband ones.¶
Semiclassical gain¶
nextnano.NEGF treats carriers by non-equilibrium Green’s functions but consider light as a classical electromagnetic field. It assumes the dipole approximation, which is valid for sub-micron period lengths and mid-infrared light.
nextnano.NEGF supports gain calculated within the NEGF formalism (default) and gain calculated from Fermi’s golden rule (semiclassical gain) (see Gain{ }). Here, we use the latter. The electric field amplitude is considered as perturbative. From Fermi’s golden rule, the absorption spectrum, namely (number of photons absorbed per unit volume per unit time) / (number of photons injected per unit area per unit time), is calculated for given electric field polarization \(\vec{\epsilon}\) and photon energy \(\hbar\omega\) [ChuangOpto1995]:
where \(e, c, m_0\) are the elementary charge, vacuum speed of light, and bare electron mass, respectively. \(\varepsilon_0\) and \(\varepsilon(\omega)\) are the vacuum permittivity and dielectric function at the photon frequency. The normalization volume \(V\) is the one of a cylinder with the length of one period and radius determined internally from LateralDiscretization{ Value } (see LateralDiscretization{ }). \(\vec{\pi}_{nm}\) is the in-plane wavevector-dependent momentum matrix elements in the eigenstates of the (reduced) Hamiltonian (see SimulationParameter{ } for the mode-space approach in nextnano.NEGF). The summation is taken over all possible transitions with positive photon energy. Due to the dipole approximation, the formula involves only the vertical transitions.
The standard deviation of the Gaussian distribution is calculated from the input parameter Semiclassic{ Linewidth } which we denote here by \(\Gamma\) (meV):
nextnano.NEGF outputs the minus of the absorption spectrum, i.e., gain spectrum in the folder (Bias)mV\Gain.
Input file settings¶
Equilibrium{Broadening} specifies the linewidth of subbands. This phenomenological input parameter replaces scattering calculation.
If Equilibrium{SplitFermi = yes}, quasi-Fermi levels for electrons and holes are set to match the potential drop per period.
Equilibrium{
Broadening = 30.0
SplitFermi = yes
}
Attention
We are extending the scattering calculation implemented for 1,2, and 3-band models to 8-band. Once implemented, the phenomenological broadening parameter will not be needed.
8-band \(\mathbf{k} \cdot \mathbf{p}\) model is used to find energy eigenstates in heterostructure. The NEGF basis is constructed from them.
Materials{
NumberOfBands = 8
}
We calculate gain spectrum using Fermi’s golden rule, which we call semiclassical gain. Multiple polarizations can be specified for one simulation.
Gain{
Semiclassic{
Linewidth = 30
}
Polarization{
Re = [1,0,0]
}
Polarization{
Re = [0,0,1]
}
}
To output in-plane k-integrated densities under the (Bias)mV\2D_plots folders, we use
Output{
PlotDispersion = 2
}
Simulation results¶
Figure 4.4.12 shows the local density of states in one period.
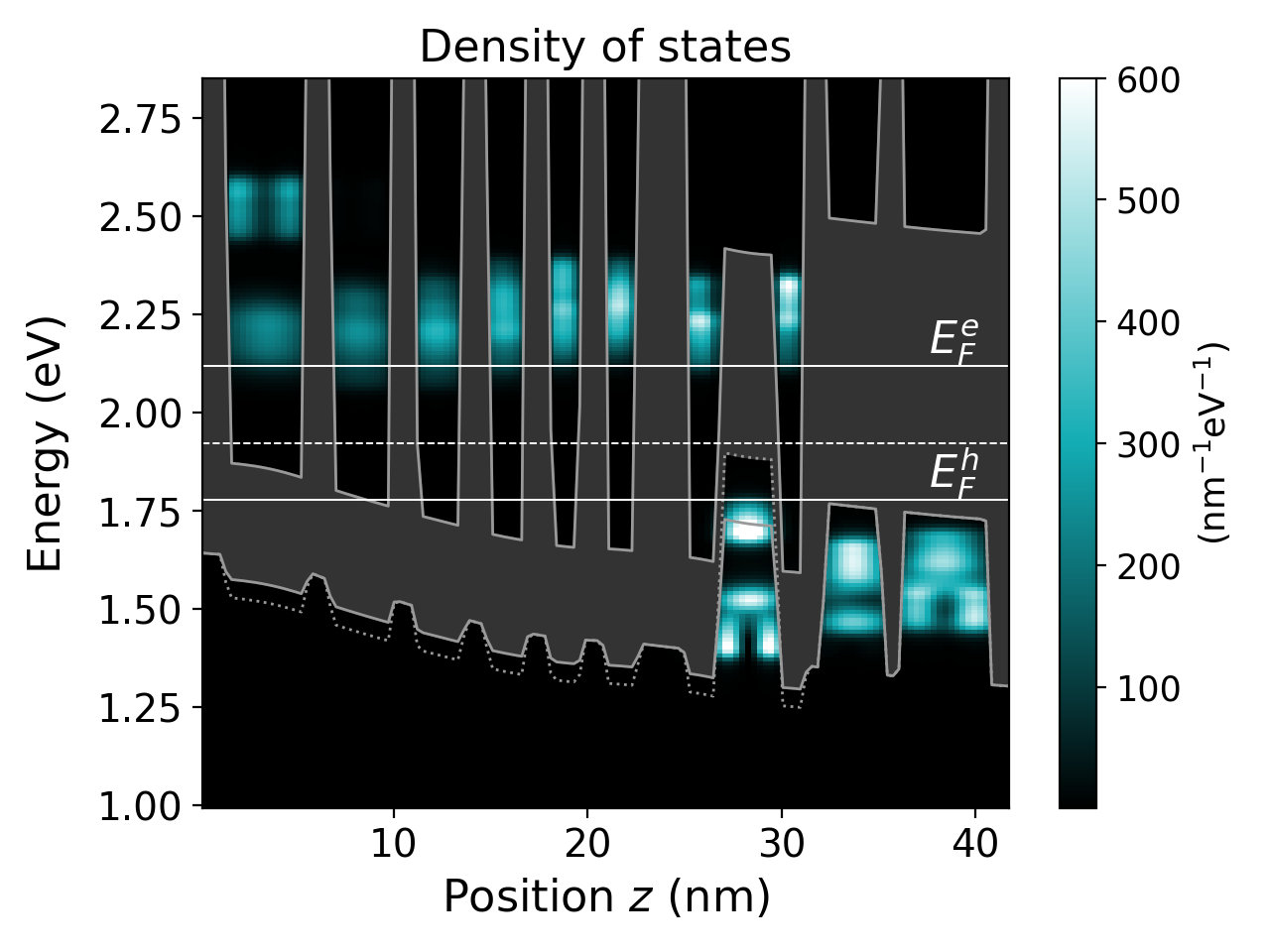
Figure 4.4.12 Band edge profile (grey lines), local density of states (colormap), quasi-Fermi levels (white solid lines) and the energy border for distinguishing electrons and holes (dashed white line). The heavy-hole band edge (dotted) is beyond the light-hole (solid) in the \(\mathrm{Ga}_{0.65}\mathrm{In}_{0.35}\mathrm{Sb}\) hole well. (Run ICL_zb_InAs-GaInSb_Vurgaftman_NatureComm_2011_quasi-equilibrium_heavyDoping_negf.negf to reproduce.)¶
The two input files ICL_zb_InAs-GaInSb_Vurgaftman_NatureComm_2011_quasi-equilibrium_*_negf.negf differ only in the doping profile. ‘Moderate doping’ and ‘Heavy doping’ refer to … in [VurgaftmanNatComm2011]. Figure 4.4.13 clearly shows the carrier rebalancing in the W-shaped quantum well.
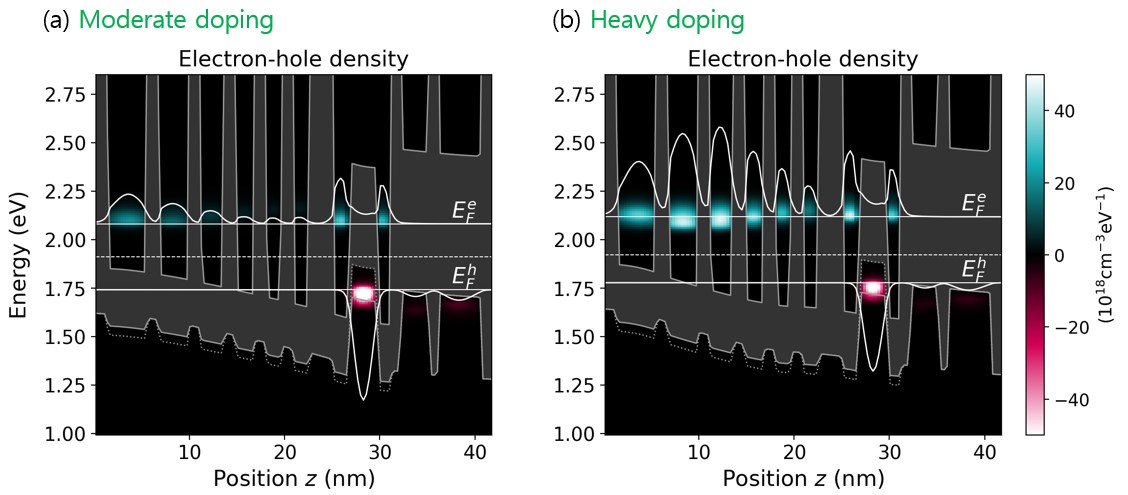
Figure 4.4.13 Energy-resolved electron and hole densities for the (a) reference and (b) optimally-doped structures at the potential drop per period of 340 mV. White curves indicate the electron and hole densities integrated above and below the border energy (dashed line). They were scaled by a common factor for (a) and (b).¶
Furthermore, nextnano.NEGF predicts that this carrier rebalancing enhances the gain at target photon energies (Figure 4.4.14). This is in agreement with the experimental observation [VurgaftmanNatComm2011].

Figure 4.4.14 Gain spectra of the structures Figure 4.4.13 (a,b), demonstrating an enhancement for the photon energies 310-330 meV. (Place plot_gain_enhancement.plt at the root of your output directory and run it to reproduce.)¶
In addition to the desired gain at the photon energies 310-330 meV, the structure has a significant absorption peak around 250 meV. Gain spectra from individual transitions are stored in (Bias)mV\Gain\SemiclassicalDecomposed_vs_Energy_(light polarization).dat (Figure 4.4.15). The state index in the file refers to the energy eigenstates, which can be found in (Bias)mV\EnergyEigenstates\EigenStates.dat. This decomposed data shows that the dip around 250 meV in Figure 4.4.14 arises from valence intersubband absorption. It has been shown to reduce the optical gain in long-wavelength mid-infrared ICLs [KnoetigLaserPhotRev2022]. The present structure, however, does not suffer from it as the heavy-hole ground states is energetically much closer to light-hole ground state than to the conduction band ground state, i.e., absorption peak occurs at lower energy than the desired lasing transition.
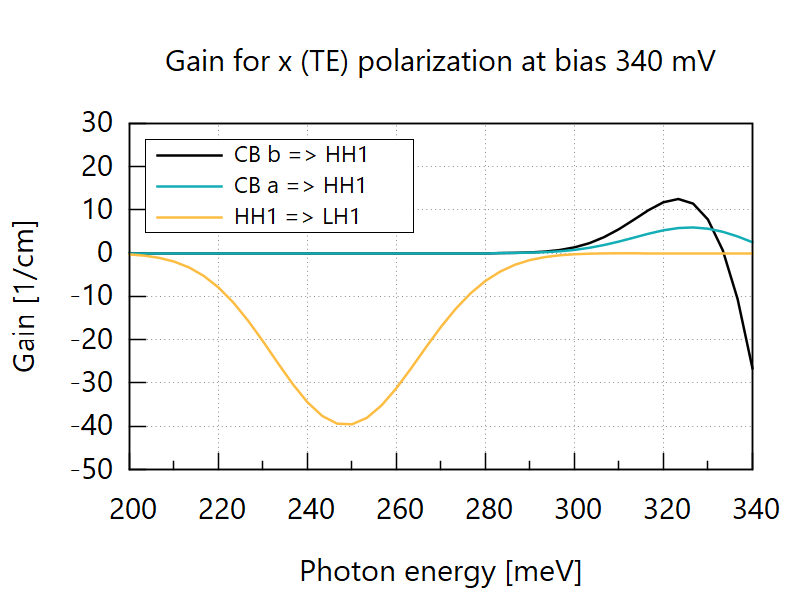
Figure 4.4.15 Relevant transitions in the gain spectrum of the heavily-doped case. ‘CB a’ and ‘CB b’ refer to the two lowest electron states in the asymmetric W-shaped quantum well. ‘HH1’ and ‘LH1’ are the valence band ground states with dominant heavy- and light-hole components at the zone center. (Place plot_gain_decomposed_x-polarization.plt at the root of your output directory and run it to reproduce.)¶
Larger bias creates more electrons and holes in the W-shaped recombination region, which increases gain (Figure 4.4.16). The gain does not saturate in the present model since the feedback from emitted light (cavity field) to carrier transport is not included.
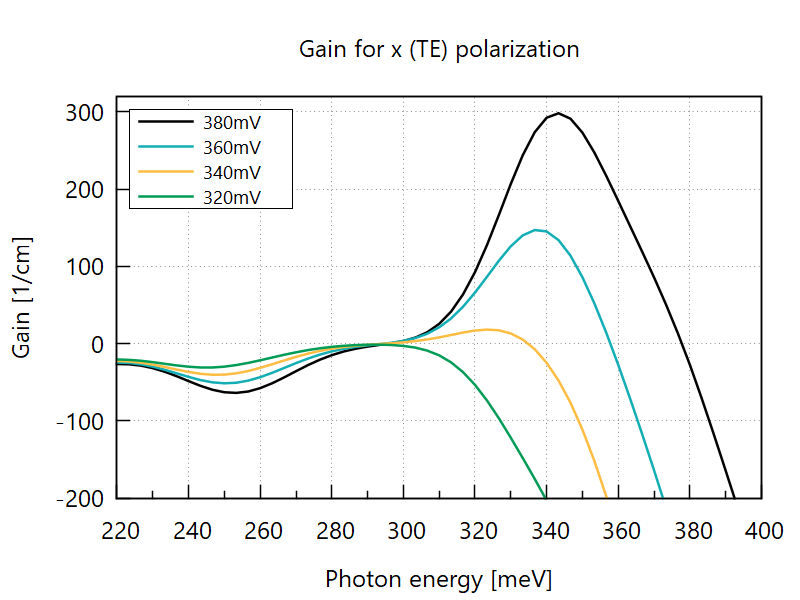
Figure 4.4.16 Gain spectra of the structure (b) of Figure 4.4.13 for various bias voltages. (Place plot_gain_vs_bias.plt at the root of your output directory and run it to reproduce.)¶
Lastly, we investigate the polarization dependence of the gain spectra. While the z (TM) polarization gives only negligible contribution to the radiative interband transition (CB => HH1), it is the dominant channel for intraband devices such as quantum cascade lasers (QCLs). In ICLs, the TM polarization manifests itself in the parasitic absorptions between the states dominated by the same spinor component (Figure 4.4.17).

Figure 4.4.17 Gain spectra of the structure (b) of Figure 4.4.13 for the TM polarization. (Place plot_gain_decomposed_z-polarization.plt at the root of your output directory and run it to reproduce.)¶
Prospects¶
This model has two major limitations.
Firstly, it relies on a phenomenological broadening parameter \(\Gamma\) in Fermi’s golden rule. However, the NEGF formalism is capable of calculating the line broadening from the first principle using fundamental material parameters. We are currently testing interband devices in the presence of interface roughness, alloy disorder, and LO phonon scattering.
The second limitation is the assumption of flat quasi-Fermi levels (Figure 4.4.11) and hence the use of equilibrium Green’s functions. This hinders charge current (electron transport) calculation. We are developing a more realistic model without this assumption to enable simulation of current-voltage characteristics as well as self-consistent calculation of carrier transport and gain.