Empirical tight-binding sp3s* band structure of GaAs, GaP, AlAs, InAs, C (diamond) and Si
The input files to be used are:
1D_TightBinding_bulk_GaAs.in
1D_TightBinding_bulk_GaAs_so.in
1D_TightBinding_bulk_Al0.3Ga0.7As.in
1D_TightBinding_bulk_GaP.in
1D_TightBinding_bulk_GaP_so.in
1D_TightBinding_bulk_AlAs.in
1D_TightBinding_bulk_AlAs_so.in
1D_TightBinding_bulk_C.in
1D_TightBinding_bulk_Si.in
1D_TightBinding_bulk_Ge.in
1D_TightBinding_bulk_InAs_so.in
1D_TightBinding_bulk_AlSb_so.in
1D_TightBinding_bulk_InSb_so.in
1D_TightBinding_bulk_Al0.5In0.5Sb.in
Empirical tight-binding sp3s* band structure of GaAs and GaP
The empirical tight-binding model that is used here is based on the sp3s* Hamiltonian, i.e. the 10 x 10 matrix given in Table (A) of [VoglJPCS1983].
In addition, we include spin-orbit coupling leading to a 20 x 20 matrix. The additional terms arising due to spin-orbit coupling are given for instance on p. R5 of [CarloSST2003].
We note that nowadays much better theoretical methods are available for calculating the band structure of bulk materials. However, for educational purposes, the chosen sp3s* method should be sufficient.
In this tutorial, we calculate the bulk band structure of
GaAs, GaP and AlAs without spin-orbit coupling using the parameters of [VoglJPCS1983] at T = 0 K
GaAs, GaP and AlAs including spin-orbit coupling using the parameters of [KlimeckSM2000] at T = 300 K
Input
The values for the tight binding parametrization have to be specified in the input file:
$numeric-control
...
!------------------------------------------------------------------------------
! Tight-binding parameters for GaAs (values of [Klimeck]). The units are [eV].
!------------------------------------------------------------------------------
!tight-binding-parameters = -3.53284d0 ! Esa (GaAs)
0.27772d0 ! Epa
-8.11499d0 ! Esc
4.57341d0 ! Epc
12.33930d0 ! Es_a
4.31241d0 ! Es_c
-6.87653d0 ! Vss
1.33572d0 ! Vxx
5.07596d0 ! Vxy
0d0 ! Vs_s_
2.85929d0 ! Vsa_pc
11.09774d0 ! Vsc_pa
6.31619d0 ! Vs_a_pc
5.02335d0 ! Vs_c_pa
0.32703d0 0.12000d0 ! Delta_so_a Delta_so_c
! Note: a = anion, c = cation
! s_ = s*
For more information about the meaning of these parameters, refer to the above cited references.
Output
The output of the calculated tight-binding band structure can be found in the following file: TightBinding/BandStructure.dat
The first column contains the number of the grid point in the Brillouin zone. These grid points run
from L point to Gamma point (along Lambda)
from Gamma point to X point (along Delta)
from X point to the U, K points
from U,K points to Gamma point (along Sigma)
The next columns are the eigenvalues of the tight-binding Hamiltonian in units of [eV] for each grid point in k = (\(k_x\), \(k_y\), \(k_z\)) space.
The file TightBinding/BandStructure_without_so.dat contains the tight-binding band structure without spin-orbit coupling.
The file TightBinding/k_vectors.dat contains for each point the information to which k point it belongs to.
no. |
kx |
ky |
kz |
|k| |
kx [2pi/a] |
ky [2pi/a] |
kz [2pi/a] |
|k| [2pi/a] |
|---|---|---|---|---|---|---|---|---|
1 |
0.314159E+01 |
0.314159E+01 |
0.314159E+01 |
0.544140E+01 |
0.500000E+00 |
0.500000E+00 |
0.500000E+00 |
0.866025E+00 |
Note: Currently the units of \(k_x\), \(k_y\) and \(k_z\) do not take into account the lattice constant a. This should be modified. The values for \(k_x\), \(k_y\) and \(k_z\) in units of [2pi/a] are correct, however. Another improvement would be to calculate and output the three-dimensional energy dispersion E(\(k_x\), \(k_z\), \(k_z\)) and two-dimensional slices E(\(k_x\), \(k_z\), 0) through the three-dimensional energy dispersion E(\(k_x\), \(k_z\), \(k_z\)) for a constant value of \(k_z\), e.g. \(k_z\) =0.
Results
GaAs without spin-orbit coupling from 1D_TightBinding_bulk_GaAs.in
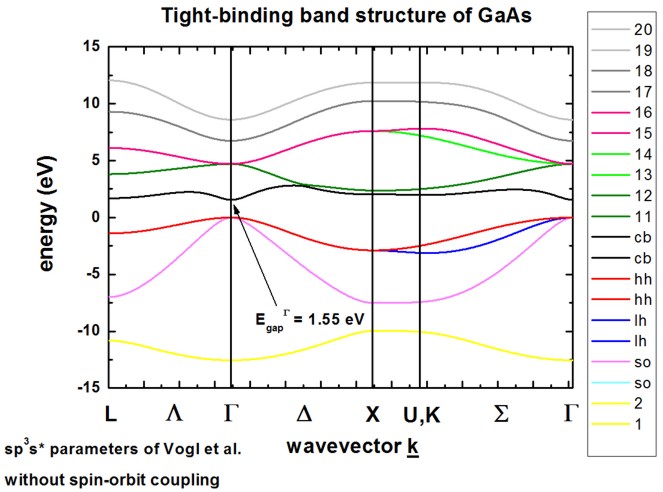
The calculated band structure is in excellent agreement with Fig. 11(d) of [VoglJPCS1983]. The conduction band minimum is at the Gamma point (direct band gap). Because spin-orbit coupling is not included in the Hamiltonian, the sp3s* empirical tight-binding parameters were taken from [VoglJPCS1983] at T = 0 K.
GaAs including spin-orbit coupling from 1D_TightBinding_bulk_GaAs_so.in
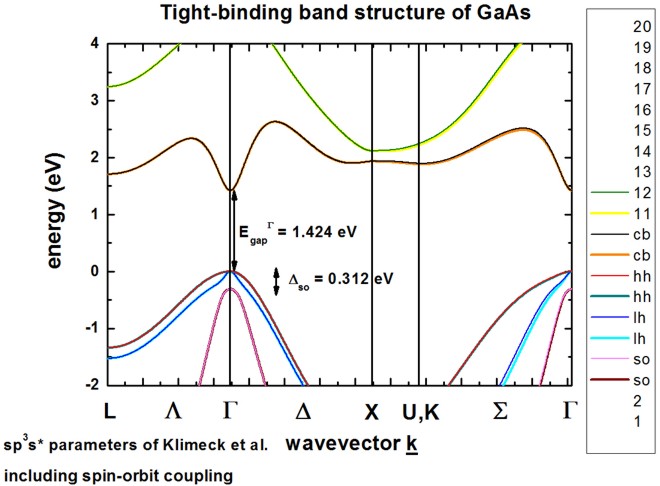
The calculated band structure is in excellent agreement with Fig. 1 of [KlimeckSM2000]. The conduction band minimum is at the Gamma point (irect band gap). Spin-orbit coupling lifts the degeneracy of heavy/light hole and split-off hole at the Gamma point. Heavy and light hole are still degerate at the Gamma point. The sp3s* empirical tight-binding parameters were taken from [KlimeckSM2000] at T = 300 K.
GaP without spin-orbit coupling from 1D_TightBinding_bulk_GaP.in
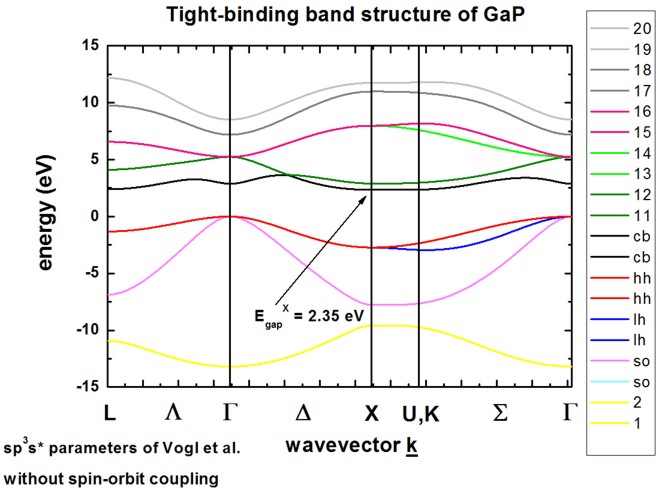
The calculated band structure is in excellent agreement with Fig. 2 of [VoglJPCS1983]. The conduction band minimum is calculated to be at the X point (indirect band gap). Because spin-orbit coupling is not included in the Hamiltonian, heavy, light and the split-off hole are degenerate at the Gamma point, i.e at k = (\(k_x\), \(k_y\), \(k_z\)) = 0. The sp3s* empirical tight-binding parameters were taken from [VoglJPCS1983] at T = 0 K.
GaP including spin-orbit coupling from 1D_TightBinding_bulk_GaP_so.in
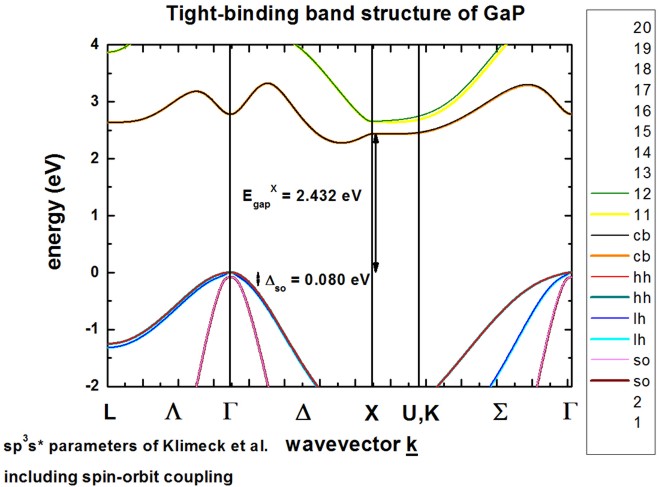
The calculated band structure is in excellent agreement with Fig. 1 of [KlimeckSM2000]. The conduction band minimum is in the vincinity of the X point at the Delta line (indirect band gap), so-called camel’s back. Spin-orbit coupling lifts the degeneracy of heavy/light hole and split-off hole at the Gamma point. Heavy and light hole are still degenerate at the Gamma point. The sp3s* empirical tight-binding parameters were taken from [KlimeckSM2000] at T = 300 K.
AlAs without spin-orbit coupling from 1D_TightBinding_bulk_AlAs.in
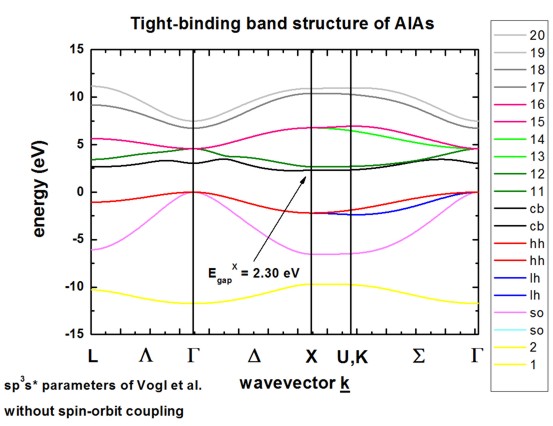
InAs including spin-orbit coupling from 1D_TightBinding_bulk_InAs_so.in

C (diamond) without spin-orbit coupling from 1D_TightBinding_bulk_C.in
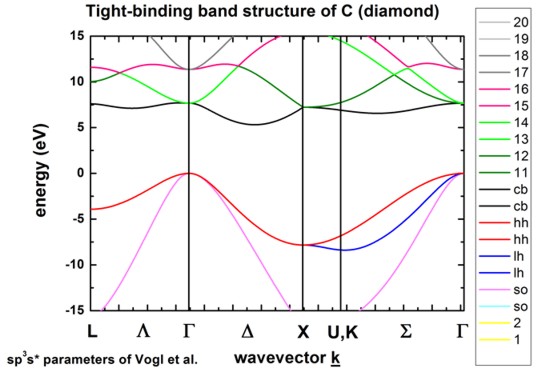
Si (silicon) without spin-orbit coupling from 1D_TightBinding_bulk_Si.in
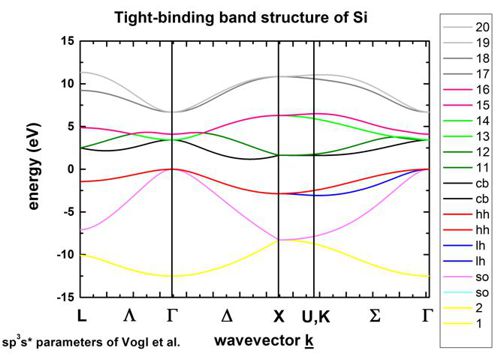
The k space resolution, i.e. the number of grid points on the axis of these plots can be adjusted. This can be done with:
$tighten
calculate-tight-binding-tighten = no
destination-directory = TightBinding/
number-of-k-points = 50 ! This number corresponds to 50 k points between the Gamma point and the X point
! The number of k points along the other directions are scaled accordingly.